链表 | Channing's Blog

链表基础知识

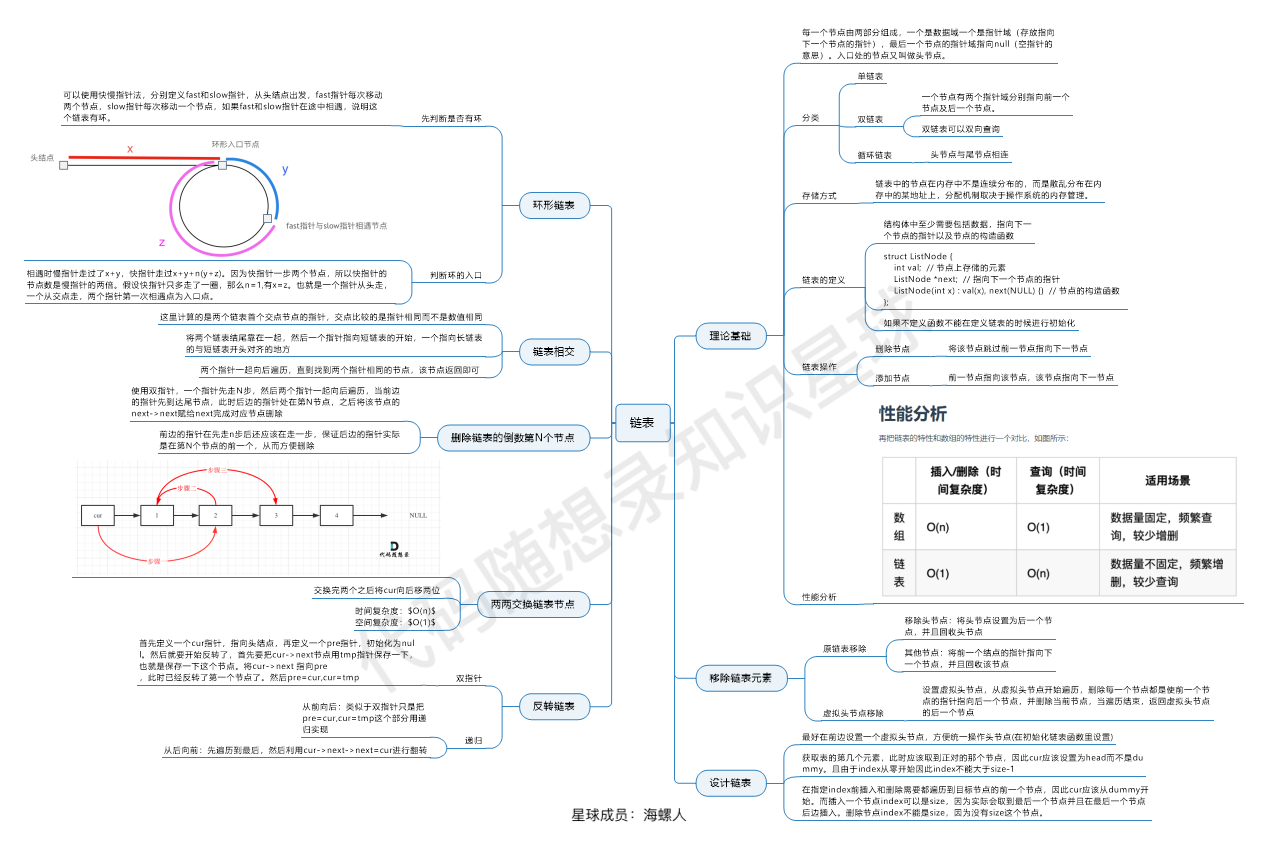
链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向nullptr（空指针）。

链表的入口节点称为链表的头结点也就是head。

如图所示：

链表的类型

接下来说一下链表的几种类型:

单链表

刚刚说的就是单链表。

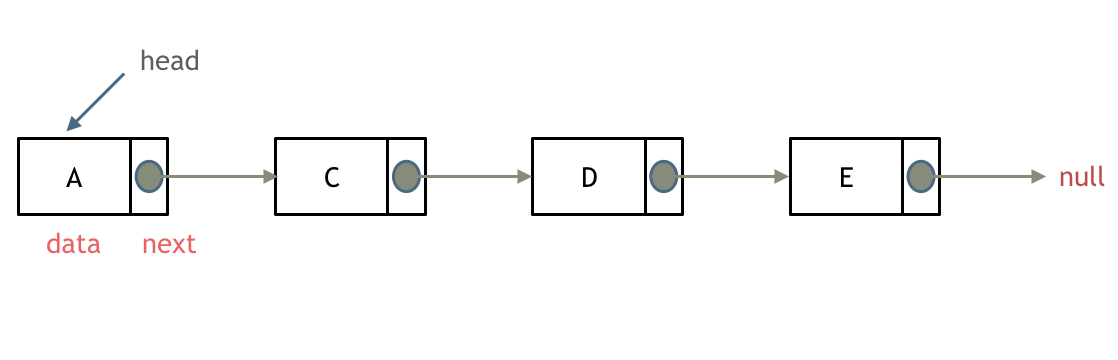
双链表

单链表中的指针域只能指向节点的下一个节点。

双链表：每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。

双链表既可以向前查询也可以向后查询。

如图所示：

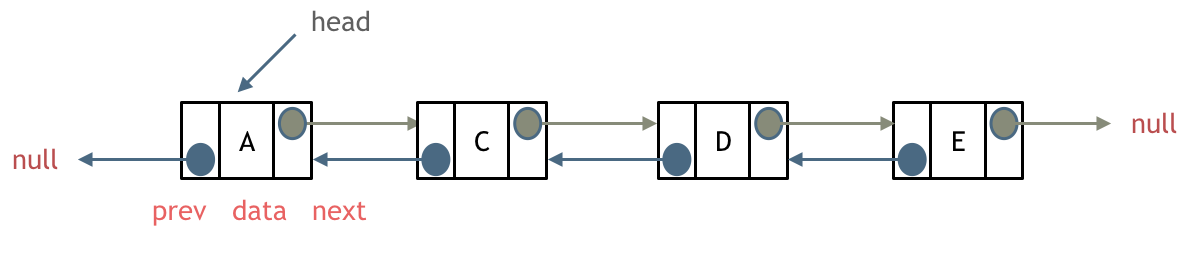
循环链表

循环链表，顾名思义，就是链表首尾相连。

循环链表可以用来解决约瑟夫环问题。

链表的存储方式

了解完链表的类型，再来说一说链表在内存中的存储方式。

数组是在内存中是连续分布的，但是链表在内存中可不是连续分布的。

链表是通过指针域的指针链接在内存中各个节点。

所以链表中的节点在内存中不是连续分布的，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。

如图所示：

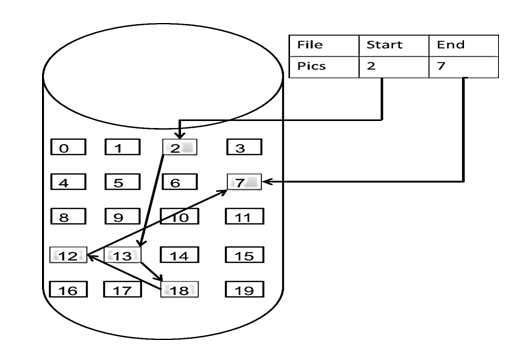
这个链表起始节点为2，终止节点为7，各个节点分布在内存的不同地址空间上，通过指针串联在一起。

链表的定义

C/C++的定义链表节点方式，如下所示：

// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(nullptr) {}  // 节点的构造函数
};

若不定义构造函数，C++默认生成一个构造函数。但这个构造函数不会初始化任何成员变量，举两个例子：

通过自己定义构造函数初始化节点：

1	ListNode* head = new ListNode(5);

使用默认构造函数初始化节点：

1 2	ListNode* head = new ListNode(); head->val = 5;

所以如果不定义构造函数使用默认构造函数的话，在初始化的时候就不能直接给变量赋值！

链表的操作

删除节点

删除D节点，如图所示：

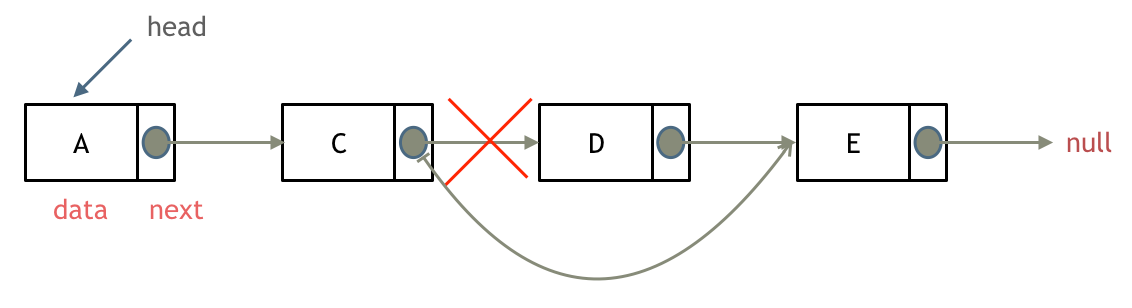
只要将C节点的next指针指向E节点就可以了。但D节点依然存留在内存里，只不过是没有在这个链表里而已。所以在C++里最好是再手动释放这个D节点，释放这块内存。delete delNode;

添加节点

如图所示：

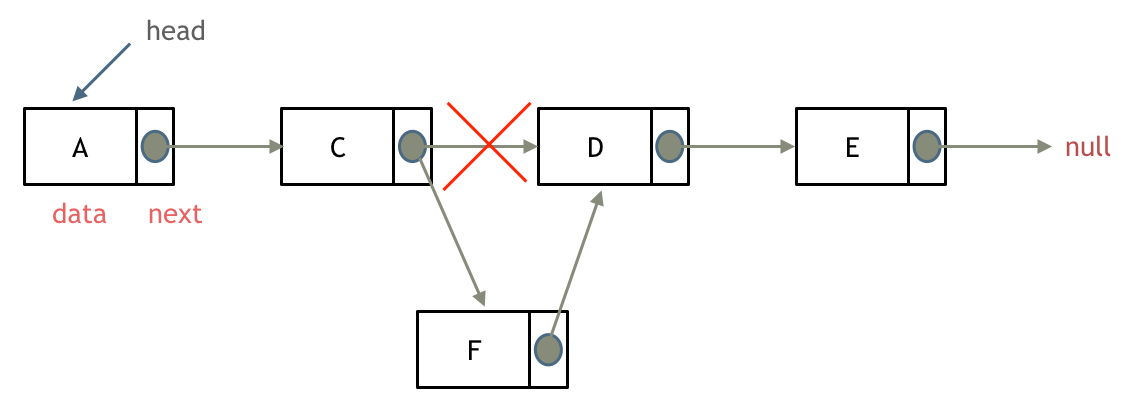
可以看出链表的增添和删除都是操作，也不会影响到其他节点。但注意，要删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是。

性能分析

再把链表的特性和数组的特性进行一个对比，如图所示：

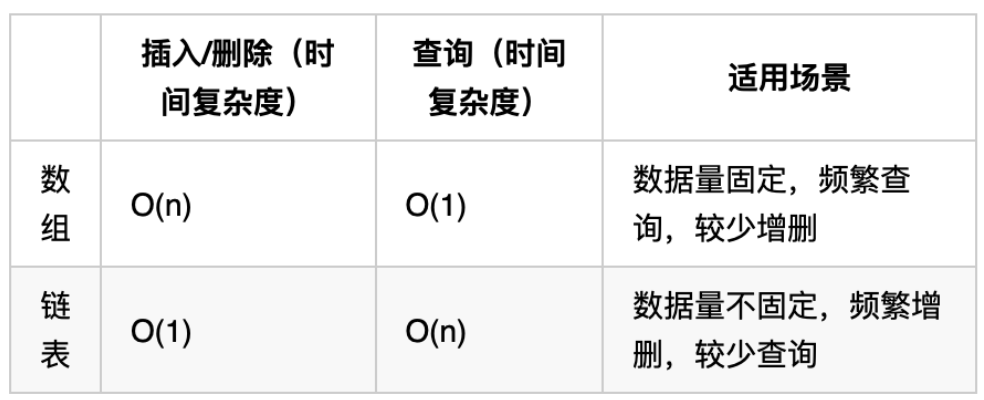
数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。

链表的长度可以是不固定的，并且可以动态增删，适合数据量不固定，频繁增删，较少查询的场景。

203.移除链表元素

力扣题目链接

题意：删除链表中等于给定值 val 的所有节点。

示例 1：
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：
输入：head = [], val = 1
输出：[]

示例 3：
输入：head = [7,7,7,7], val = 7
输出：[]

C++代码

直接使用原来的链表来进行移除节点操作：

时间复杂度:
空间复杂度:

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 删除头结点
        while (head != nullptr && head->val == val) { // 注意这里不是if
            ListNode* tmp = head;
            head = head->next;
            delete tmp;
        }

        // 删除非头结点
        ListNode* cur = head;
        while (cur != nullptr && cur->next!= nullptr) {
            if (cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            } else {
                cur = cur->next;
            }
        }
        return head;
    }
};

设置一个虚拟头结点在进行移除节点操作：

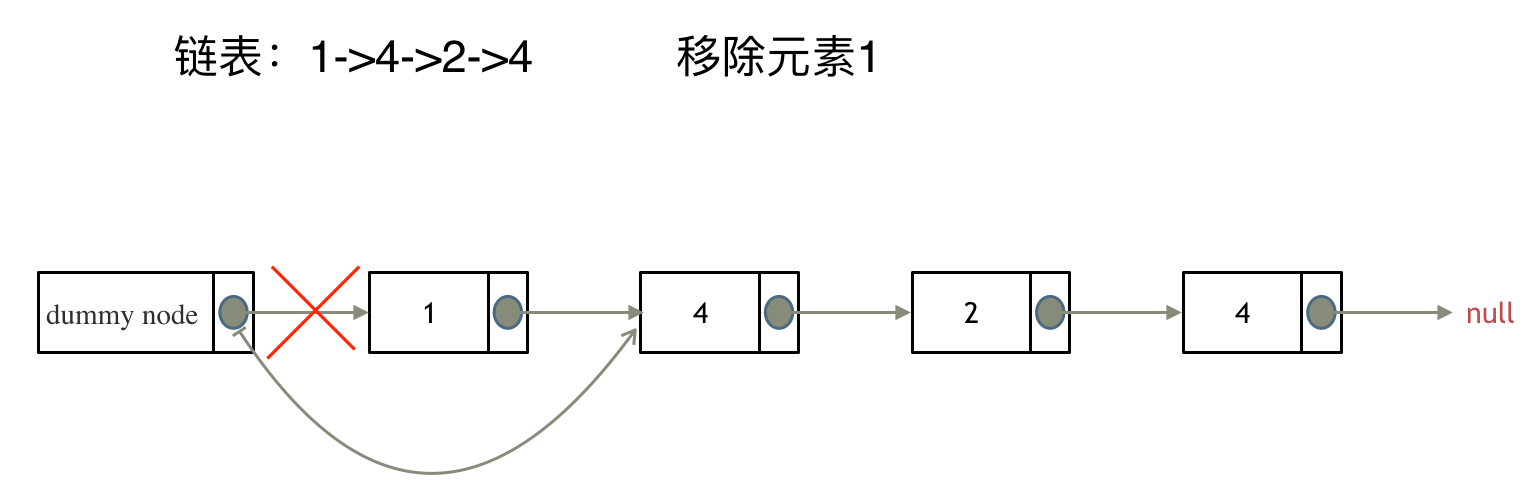
时间复杂度:
空间复杂度:

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
        ListNode* cur = dummyHead;
        while (cur->next != nullptr) {
            if(cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            } else {
                cur = cur->next;
            }
        }
        head = dummyHead->next;
        delete dummyHead;
        return head;
    }
};

707.设计链表

力扣题目链接

题意：

在链表类中实现这些功能：

get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

时间复杂度: 涉及 index 的相关操作为 , 其余为
空间复杂度:

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptrptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptrptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        //delete命令指示释放了tmp指针原本所指的那部分内存，
        //被delete后的指针tmp的值（地址）并非就是nullptr，而是随机值。也就是被delete后，
        //如果不再加上一句tmp=nullptrptr,tmp会成为乱指的野指针
        //如果之后的程序不小心使用了tmp，会指向难以预想的内存空间
        tmp=nullptrptr;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptrptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

206.翻转链表

力扣题目链接

题意：反转一个单链表。

示例:
输入: 1->2->3->4->5->nullptr
输出: 5->4->3->2->1->nullptr

双指针法

时间复杂度:
空间复杂度:

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = nullptr;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

递归法

递归法相对抽象一些，但是其实和双指针法是一样的逻辑，同样是当cur为空的时候循环结束，不断将cur指向pre的过程。

关键是初始化的地方，可能有的同学会不理解，可以看到双指针法中初始化 cur = head，pre = nullptr，在递归法中可以从如下代码看出初始化的逻辑也是一样的，只不过写法变了。

具体可以看代码（已经详细注释），双指针法写出来之后，理解如下递归写法就不难了，代码逻辑都是一样的。

时间复杂度: , 要递归处理链表的每个节点
空间复杂度: , 递归调用了 n 层栈空间

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == nullptr) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = nullptr;
        return reverse(nullptr, head);
    }

};

可以发现，上面的递归写法和双指针法实质上都是从前往后翻转指针指向，

其实还有另外一种与双指针法不同思路的递归写法：从后往前翻转指针指向。具体代码如下（带详细注释）：

时间复杂度:
空间复杂度:

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 边缘条件判断
        if(head == nullptr) return nullptr;
        if (head->next == nullptr) return head;
        
        // 递归调用，翻转第二个节点开始往后的链表
        ListNode *last = reverseList(head->next);
        // 翻转头节点与第二个节点的指向
        head->next->next = head;
        // 此时的 head 节点为尾节点，next 需要指向 nullptr
        head->next = nullptr;
        return last;
    }
};

使用虚拟头结点解决链表翻转

// 迭代方法：增加虚头结点，使用头插法实现链表翻转
public static ListNode reverseList1(ListNode head) {
    // 创建虚头结点
    ListNode dumpyHead = new ListNode(-1);
    dumpyHead.next = nullptr;
    // 遍历所有节点
    ListNode cur = head;
    while(cur != nullptr){
        ListNode temp = cur.next;
        // 头插法
        cur.next = dumpyHead.next;
        dumpyHead.next = cur;
        cur = temp;
    }
    return dumpyHead.next;
}

24.两两交换链表中的节点

力扣题目链接

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

思路

建议使用虚拟头结点，不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。

对虚拟头结点的操作，还不熟悉的话，可以看这篇链表：听说用虚拟头节点会方便很多？。

接下来就是交换相邻两个元素了，此时一定要画图，不画图，操作多个指针很容易乱，而且要操作的先后顺序

初始时，cur指向虚拟头结点，然后进行如下三步：

操作之后，链表如下：

看这个可能就更直观一些了：

C++代码

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
        ListNode* cur = dummyHead;
        while(cur->next != nullptrptr && cur->next->next != nullptrptr) {
            ListNode* tmp = cur->next; // 记录临时节点
            ListNode* tmp1 = cur->next->next->next; // 记录临时节点

            cur->next = cur->next->next;    // 步骤一
            cur->next->next = tmp;          // 步骤二
            cur->next->next->next = tmp1;   // 步骤三

            cur = cur->next->next; // cur移动两位，准备下一轮交换
        }
        return dummyHead->next;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

19.删除链表的倒数第 N 个结点

力扣题目链接

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：

输入：head = [1], n = 1
输出：[]
示例 3：

输入：head = [1,2], n = 1
输出：[1]

分为如下几步：

首先这里我推荐大家使用虚拟头结点，这样方便处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇：链表：听说用虚拟头节点会方便很多？
定义fast指针和slow指针，初始值为虚拟头结点，如图：

fast首先走n + 1步，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：

fast和slow同时移动，直到fast指向末尾，如题：

删除slow指向的下一个节点，如图：

双指针法

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 虚拟头节点
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;

        // 双指针指向虚拟头结点
        ListNode* slow = dummyHead;
        ListNode* fast = dummyHead;

        n = n + 1;
        // 将快指针向后移动n+1个位置，为了让fast与slow之间隔着n个节点
        while (n--) 
        {
            fast = fast->next;
        }

        // 同时移动双指针
        while (fast != nullptrptr)
        {
            slow = slow->next;
            fast = fast->next;
        }

        // 删除slow后面的节点
        slow->next = slow->next->next;
        return dummyHead->next;
    }
};

160. 链表相交

力扣题目链接

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 nullptr 。

图示两个链表在节点 c1 开始相交：

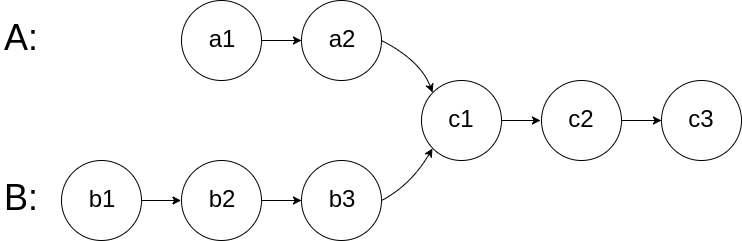
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须保持其原始结构。

思路

简单来说，就是求两个链表交点节点的指针。这里同学们要注意，交点不是数值相等，而是指针相等。

为了方便举例，假设节点元素数值相等，则节点指针相等。

看如下两个链表，目前curA指向链表A的头结点，curB指向链表B的头结点：

求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB 末尾对齐的位置，如图：

此时就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。

否则循环退出返回空指针。

C++代码

时间复杂度：
空间复杂度：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != nullptr) { // 求链表A的长度
            lenA++;
            curA = curA->next;
        }
        while (curB != nullptr) { // 求链表B的长度
            lenB++;
            curB = curB->next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            swap (lenA, lenB);
            swap (curA, curB);
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap--) {
            curA = curA->next;
        }
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != nullptr) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return nullptr;
    }
};

142.环形链表

力扣题目链接

题意：
给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 nullptr。

为了表示给定链表中的环，使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

快慢指针

这道题目，不仅考察对链表的操作，而且还需要一些数学运算。

主要考察两知识点：

判断链表是否环

判断链表是否包含环属于经典问题了，解决方案也是用快慢指针：

每当慢指针 slow 前进一步，快指针 fast 就前进两步。如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast超过了 slow 一圈，说明链表中含有环。

如果有环，如何找到这个环的入口

可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

为什么要这样呢？这里简单说一下其中的原理。

假设快慢指针相遇时，慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步：

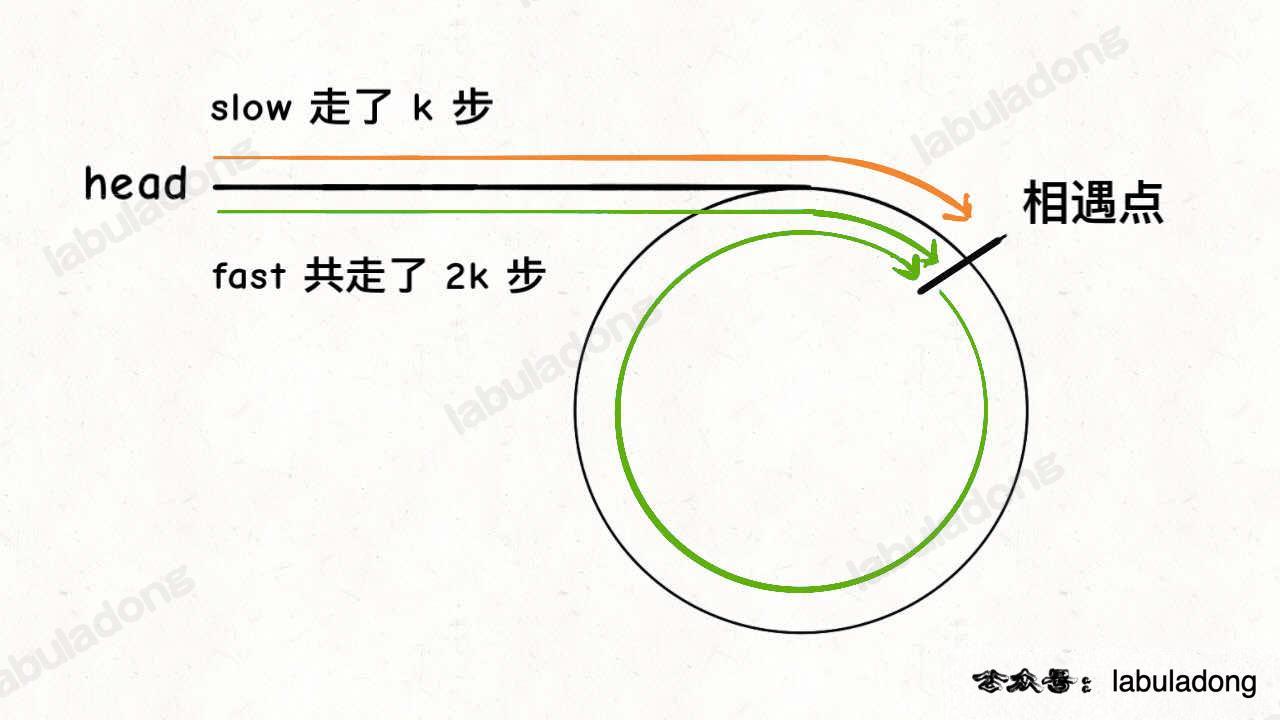
fast 一定比 slow 多走了 k 步，这多走的 k 步其实就是 fast 指针在环里转圈圈，所以 k 的值就是环长度的整数倍。

假设相遇点距环的起点的距离为 m，那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。因为结合上图的 fast 指针，从相遇点开始走k步可以转回到相遇点，那走 k - m 步肯定就走到环起点了：

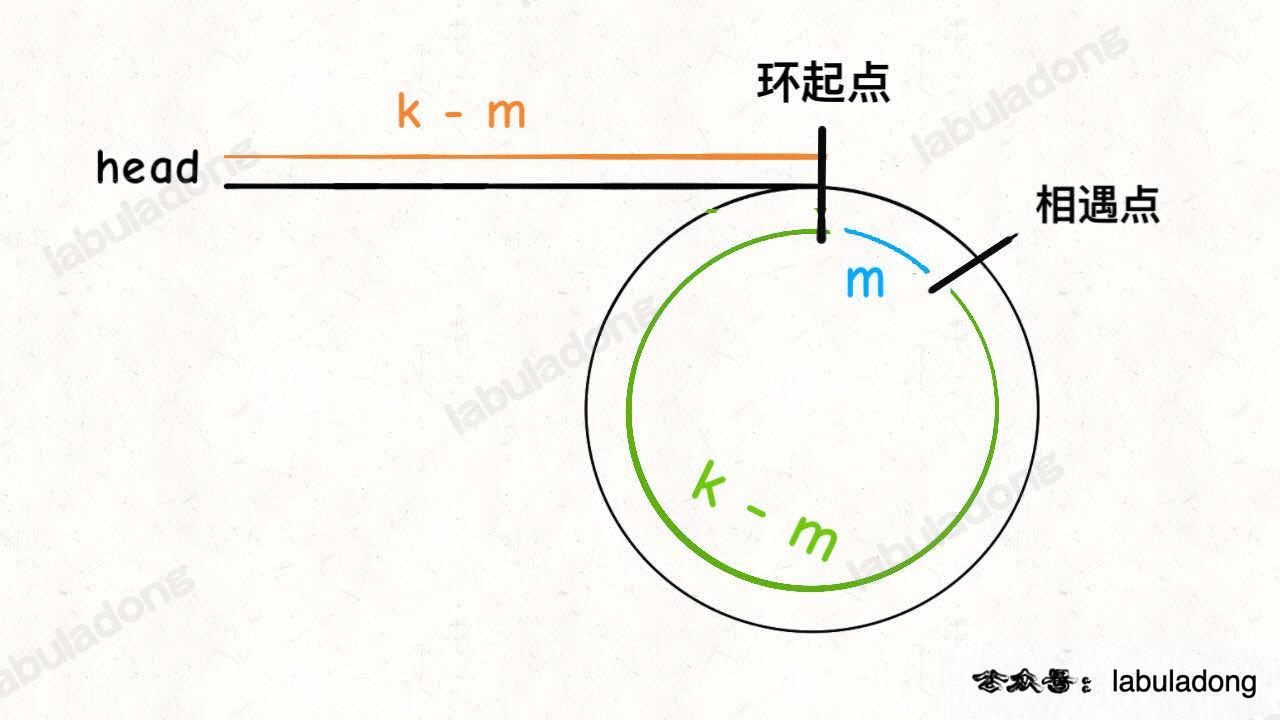
所以，只要把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。

代码如下：

时间复杂度: O(n)
- 快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
空间复杂度: O(1)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(nullptr) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇
            if (slow == fast) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2; // 返回环的入口
            }
        }
        return nullptr;
    }
};

链表总结篇

理论基础

链表的种类主要为：单链表，双链表，循环链表
链表的存储方式：链表的节点在内存中是分散存储的，通过指针连在一起。
链表是如何进行增删改查的。
数组和链表在不同场景下的性能分析。

经典题目

虚拟头结点

链表的一大问题就是操作当前节点必须要找前一个节点才能操作。这就造成了，头结点的尴尬，因为头结点没有前一个节点了。

每次对应头结点的情况都要单独处理，所以使用虚拟头结点的技巧，就可以解决这个问题。

链表的基本操作

在链表：一道题目考察了常见的五个操作！中，通设计链表把链表常见的五个操作练习了一遍。

这是练习链表基础操作的非常好的一道题目，考察了：

获取链表第index个节点的数值
在链表的最前面插入一个节点
在链表的最后面插入一个节点
在链表第index个节点前面插入一个节点
删除链表的第index个节点的数值

反转链表

在链表：听说过两天反转链表又写不出来了？中，讲解了如何反转链表。反转链表是面试中高频题目，很考察面试者对链表操作的熟练程度。给出了两种反转的方式，迭代法和递归法。建议大家先学透迭代法，然后再看递归法，因为递归法比较绕，如果迭代还写不明白，递归基本也写不明白了。可以先通过迭代法，彻底弄清楚链表反转的过程！

删除倒数第N个节点

在链表：删除链表倒数第N个节点，怎么删？中结合虚拟头结点 和双指针法来移除链表倒数第N个节点。

链表相交

链表：链表相交使用双指针来找到两链表的交点（引用完全相同，即：内存地址完全相同的交点）

环形链表

讲解了在链表如何找环，以及如何找环的入口位置。

这道题目可以说是链表的比较难的题目了。但代码却十分简洁，主要在于一些数学证明。